Immutability is a powerful concept. You don’t have to worry about whom you pass a value to. Whoever else has the same value as you does not have to worry about what you do. A computation based on a value will always lead to the same result. More concrete, if thread A passes a value to thread B there is no need to worry about what B does with the value. It can’t affect A since it will always stay the same. What if you combine two values to a composite value, do the same properties hold? The answer is yes. It can still be safely shared. As long as you stack immutable values on top of each other the resulting composite value or object will still be immutable. You can go home, come back the next day and nothing has changed.
Can you do the same with mutable objects? If thread A passes a mutable object to thread B and then performs a computation based on it’s content. Will it always lead to the same result? Will it even lead to a result? We don’t know. What if A needs to divide by a number in that object and B did change it to 0. Great, we just destroyed the universe! So we need some sort of locking mechanism to prevent B from changing the object before A made it’s computation. Or do we just need to prevent B from making changes while we check that the content is not 0 and perform our computation? What is the behaviour if you want to copy an object? Do you just copy the references in it? Do you traverse the entire object graph and copy everything in it? Something in between? After we went through all the effort to make everything work with our mutable objects, can we safely stack them together to a new object and use it somewhere else? No, we have to do everything over again! ¹

Not many developers would argue with that. However, if asked why they don’t use immutable data structures as a default you get a variety of answers. Mutability is not a problem if you know what you’re doing. Bad performance because you need to copy an object if you want to make a change to it. It’s easier to move an object 1 cm to the left than it is to bootstrap a universe where the object happens to 1 cm to the left. The first point is not going to be addressed in this article since it’s hard to argue about it. The second point, i.e. performance, is what we’re going to look at. At least in a Java world there is some truth to it. The same holds for most other traditionally non-functional languages. Even though the impact of object creation is often overestimated it can’t be argued that without the help of additional tools and only the standard Collections API, things become tedious and inefficient. The only tool provided to get something that’s close to an immutable collection is to obtain an unmodifiable view of an existing collection.

List<String> someList = new ArrayList();
someList.add("foo");
someList.add("bar");
List<String> unmodifyableList = Collections.unmodifiableList(someList);

Let’s ignore the fact that this does not guarantee that the list really isn’t modified. What needs to happen if we want to add something to this list? We make a copy of this list with the new element.

List<String> modified = new ArrayList(unmodifyableList);
modified.add("baz");
List<String> immutableModified = Collections.unmodifiableList(modified);

Great, now we have two complete lists in memory. Not to mention the time it takes to make the copy. Even some very accomplished engineers think that this is just how things work and there’s not much we can do about it. Most know that there are implementations that make it easier to construct and and work with immutable lists, such as Guava’s Immutable Collections, which even have some basic functionality to avoid unnecessary copying. From the documentation (as of version 23):

ImmutableSet<String> foobar = ImmutableSet.of("foo", "bar", "baz");
thingamajig(foobar);

void thingamajig(Collection<String> collection) {
   ImmutableList<String> defensiveCopy = ImmutableList.copyOf(collection);
   ...
}

In this example, ImmutableList.copyOf will return a view on foobar which means we only have one collection in memory. That’s an improvement, but what if an element needs to be added to the collection? Unfortunately we’re back to having two copies, the original and the new one with an additional element, including the overhead to create the copy. So as soon as performance becomes remotely important, we go back to our messy world of having a bunch of threads violate shared mutable state. But that doesn’t have to be!

Structural Sharing

From this point onward, the assumption is that everything is immutable.
The key to more efficient immutable data structures is that we don’t need complete copies to express different states if some of the structure is identical. Consider the simplest case, a list. We don’t need two complete lists to express the fact that we added an element to to list A. It’s sufficient if I tell you that B is list A plus the new element. This is straightforward to implement as a linked list.

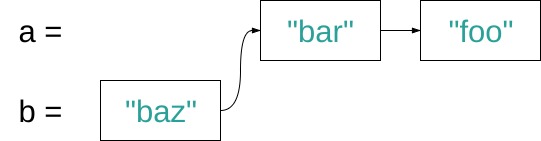
In the above example, a holds a reference to the bar node. If you traverse the list you get "bar", "foo". We now want to add an element "baz" to the beginning of the list and assign the new list to b. It’s sufficient to create a "baz" node and point it to the "bar" node of list a. If you traverse b you get "baz", "bar", "foo". Since everything is immutable we don’t have to worry about what someone with a reference to a might do. Similarly to prepending an item it is also possible to remove one. The following example shows how to create a new list c which is b with it’s first item removed.

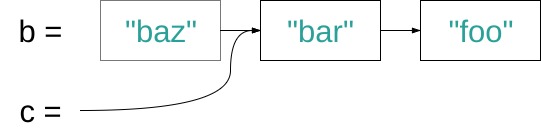
This is called structural sharing because all three lists share the nodes "foo" and "bar". So far it’s possible to prepend an item to a list in constant time, O(1) to be more specific. The same holds for removing the first item. That’s pretty great, but as soon as add or remove operations are performed on items other than the head, i.e. the first element of the list, things are starting to get worse.

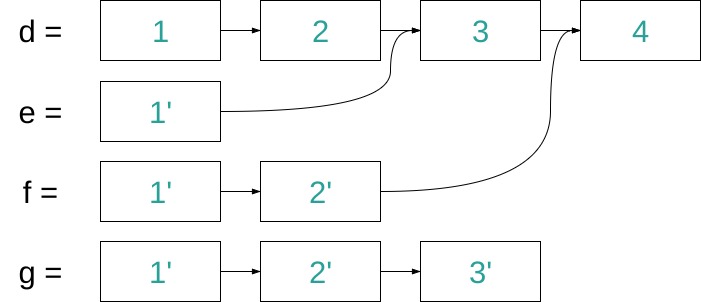
The above example shows the necessary structure to remove the elements 2-4 and assign the resulting lists to e-g, respectively. It can be observed that both time and space complexity deteriorate the further to the end of the list the element to be removed is, to the point where we have linear time complexity of O(n) and no structural sharing between the different lists any more. Add operations work in a similar way and suffer from the same performance loss.
To summarise. So far we have an immutable linked list that makes use of structural sharing. Best-case performance is O(1) on add/remove operations with 100% structural sharing, i.e. 0% additional memory compared to it’s mutable counterpart. Worst-case performance is O(n) with 0% structural sharing when operations are performed on the last element. This allows for an efficient implementation of a stack data structure, however, it primarily serves as an easy to understand example of an immutable persistent data structure. The goal is to have implementations of more commonly used structures, like lists and maps. The following sections explore more sophisticated implementations which almost reach, or in some edge-cases even surpass, the performance of traditional, mutable implementations.

More Efficient Implementations

The previous section established that structural sharing leads to more efficient implementations of immutable persistent data structures compared to copying everyting. In order for update operations to be efficient, we have to recycle as much of the old structe as we possibly can. A data structre that allows for more sophisticated structural sharing is the directed acyclic graph (DAG). That’s a graph with directed edges and no cycles. When traversing a DAG, if you visit a node you will never visit the same node again. A tree, for example, is a DAG (but not all DAGs are trees!). In fact, the linked list is also a DAG, albeit not a very usedful one for our pupose.
In the next example you’ll see a tree in which a node f is modified. To achieve the modification, the majority of nodes of the original tree can be retained in the new tree with root node d'.

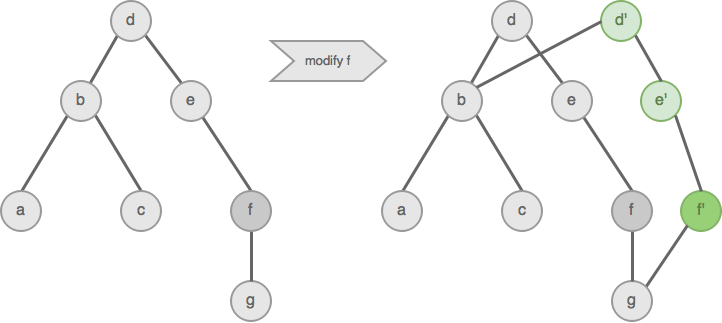
There is also something else that’s interesting about the above tree. If it is traversed with depth-first in-order traveral you’ll get a,b,c,d,e,f,g. That’s very much intended. If we construct a tree the right way we can get the nodes in any order we want. That property allows us to implement a list interface with a tree. We can still expose an interface like myList.get(3), but under the hood, the implementation is a tree. In a naive implementation, we traverse the tree until we’ve evaluated the fourth node to get the fourth element.
How does this compare to our linked list example from earlier? Assume the last element (g) has to be removed from the list, an operation with very bad performance in the linked list. Three new nodes need to be created, f' that does not point to g anymore, e' which points to f' and d' which points to e'. The new list/tree shares 50% of the structure of the old one and it took only three steps (i.e. all nodes on the path from the node in question to the root node). In case of a binary tree, the worst-case time complexity to manipulate a node is log2n, which can and generally should be written as O(log n). Since we will encounter trees with significantly larger branching factors the base is important and will be included in all expressions of complexity. Worst-case memory overhead is 50%. That’s great, but still not good enough compared to a mutable array that has O(1) complexity for most operations. The next sections will explain some implementations, minus some tweaks, that can actually be found in languages like Scala or Clojure.

Bitmap Vector Trie

There is a kind of a DAG called a trie (often pronounced “tree” from reTrieve), which is discribed quite well on Wikipedia. It’s a tree which stores all the values in the leafes, and all decendants of a node share a common prefix, e.g. a bitmap. A trie can be used to implement a list, which is called a bitmap vector trie. Nodes and leafes are arrays. The nodes hold references, either to other nodes or to leafes that hold the actual elements of the list.
Assume we want to retrieve the the element at position 50 of a list. To do so we take the bitmask of the position: 110010. Then we take the first two bits, look for the element at position 11 in the array representing the root node and follow the reference at that position to the next node. We take the next two bits, look for the element at position 00 of the current node and follow the reference to find the leaf node where the element is located. In the array representing the leaf, the element is located at position 10. Following is a visualisation of the example.

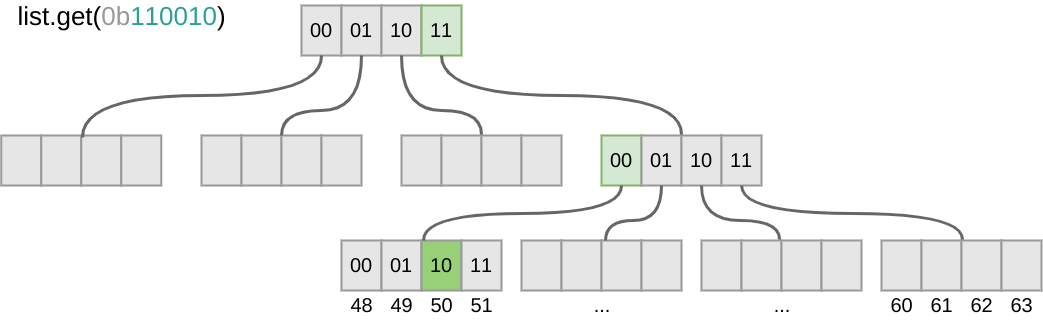
In this example the bitmap size is 6 bits with 2-bit dispatching, meaning that each layer of the tree needs an array of size 2² and two bits at the time are used to find the position in the node/leaf. That is by no means a limitation. Any bitmap size can be used to construct a bitmap vector trie. In practice, it is usually 32 because that corresponds to a 32-bit integer². A bitmap vector trie with branching factor of 32 has a time complexity of log32n to retrieve an element. That means it takes 2 operations to retrieve an item from a list of size 1000, or 6 operations to retrieve an item from a list of size 1’000’000’000. At most 7 arrays need to be reconstructed for any modifying operation on the trie. To put this into perspective, a fully initialised bitmap trie with support for 32bit integer positions has 134’217’728 nodes/leafes. Note that growing most traditional implementation of array lists isn’t free either. Oracle’s array list, for example, roughly grows like this once it’s capacity limit is hit (remember, growing includes copying the entire array):
int newCapacity = oldCapacity + (oldCapacity >> 1);³
That’s subject to change since it’s not part of the contract. The documentation only states that the details of the growth policy are not specified beyond the fact that adding an element has constant amortized time cost. ⁴
With the performance of the bitmap vector trie demonstrated above you need to put forward strong evidence as to why a shared mutable list should be used over an immutable one.

Hash Array Mapped Trie (HAMT)

So far everything was about exposing a list interface. What about an associative data type, such as a map? It’s straightforward to create a naive implementation of a hash table on top of any list, the bitmap vector trie described earlier is no exception. That implementation is called a hash array mapped trie (HAMT). All that is needed is a hash function with signature (object) => int32. To store a key-value pair, we call hash(key) which results in number, say 1337. Then we store the value at position 1337 in the underlying list. To retrieve a value, hash(key) key is called, we get 1337 as the has code and retrieve the value stored at position 1337.
In order to avoid having to initialise an array of size 2³², traditional implementations use a concept called buckets. A bucket stores values in a range of the hash space. The following illustration shows you can divide a hash space of 32 into 4 buckets.

bucket       1        2       3        4
        |--------|--------|--------|--------|
hash        0-7     8-15    16-23     24-31

This has the advantage that only a list of size 4 needs to be initialised instead of 32. However, if there are multiple values in the same bucket, the hashes of all existing values in the bucket need to be recomputed on both storing and retrieval operations. For example, if a value A has a hash code of 9 it will be put into bucket 2. If another value, B, has a hash code of 15 it will also end up in bucket 2. But in order to make sure it’s not already there, the hash code of A needs to be recomputed. Because that’s expensive, the buckets have to be resized once there are too many values in there. The resizing operation is again very expensive.
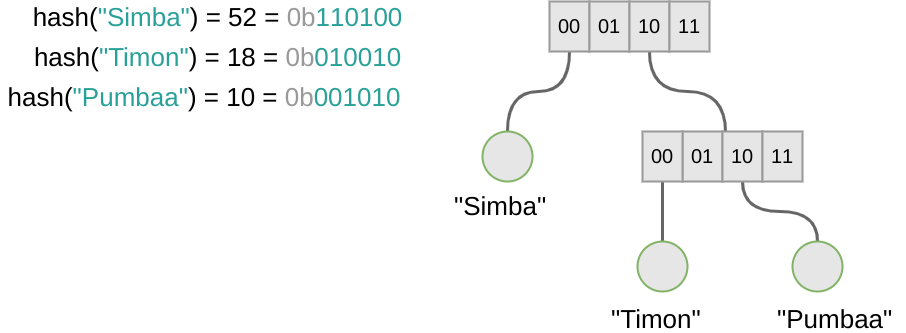
HAMTs don’t need this kind of abstraction and can grow organically. In order to do so we start using the least significant bits instead of the most significant ones to define the position of an element in the tree. What that means is we start from the right side of the bitmask instead of the left. Consider a map where The Lion King characters are being stored.

If Simba needs to be stored with his name as the key, the following happens.

1. `hash(“Simba”) = 52 = 110100
2. The two least significant bits are taken (the first two bits from the right): 00
3. We look at position 00 in the root node. Nothing is there so we can store it.

Retrieval works in a similar manner. Then we add Timon, hash("Timon") = 18 = 010010, nothing at position 10 in the root node so we just add it. Next is, of course, Pumbaa. So we do hash("Pumbaa") = 10 = 001010. Oops, position 10 is already used up by Timon. That’s not a problem. Remember, the root node has to be recreated anyway since we’re still talking about immutable persistent data structures. So we can just do the following.

This way a map can be gracefully grown. At position 10 of the root node where the conflict arised we replace the entry with a reference to another array. If a level needs to be added, more bits of the bitmask are needed to find the value associated with a key. For Timon and Pumba it is now the 4 least significant bits, for Simba still only 2.
While insert and delete operations still have comparable complexity to the bitmap vector trie we face a different problem with the HAMT. Memory usage. A good hash function will return evenly distributed hashes over the whole hash range. While that is a desired property, it poses a problem. After inserting some elements we’ll end up with a very sparsely populated tree, which means that there will be a lot of arrays in memory with only a few entries. If we use arrays of size 32 and there is only 1 entry in an array, we waste almost 97% of the allocated memory. See the following example.

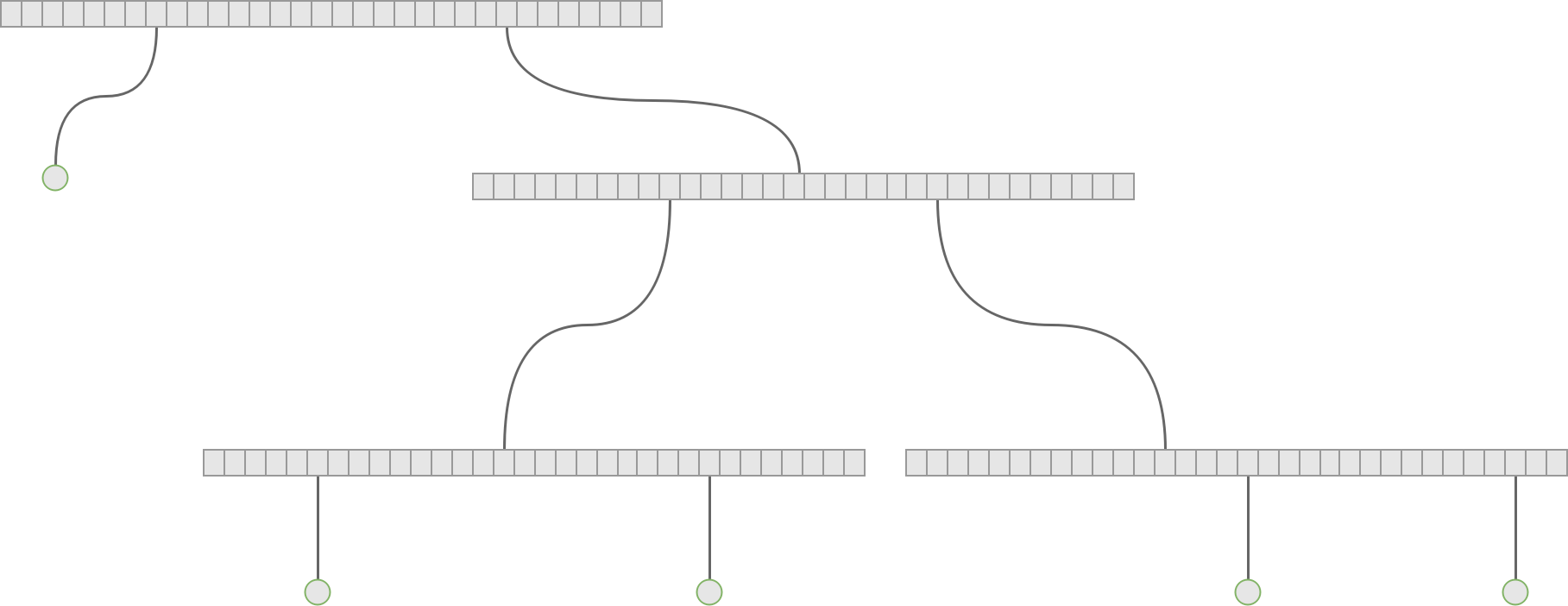
In order for the HAMT to be usable in practice the memory usage has to be reduced drastically.

Compression

Phil Bagwell suggested compressing the information in each node of the trie to reduce memory consumption.⁵ The compression works by storing the bitmask of an n-bit integer to indicate which slots of the array that stores references to the child elements of the node are used. The following example shows how a node from the previous example can be compressed.

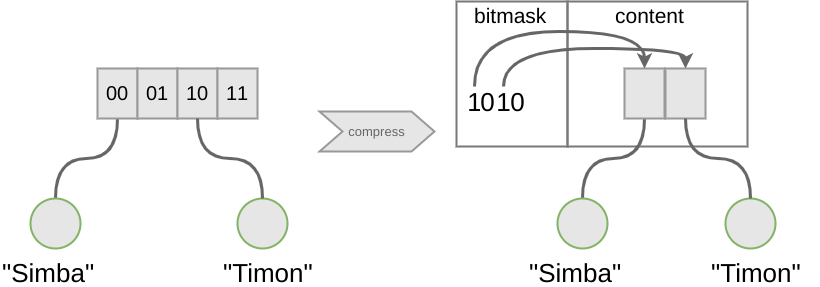
The bitmask has the size of the amount of elements that can be stored in a node, which is 4 in this example or 32 in most real world implementations. Every bit set to 1 indicates that the element at the according position in the original array would have been present. This way we only have to count the 1s and initialize an array of a size that corresponds to the sum of 1s. The first 1 corresponds to the first element of the array, the second to the second element, and so on. So we can save the space all the empty array elements wasted, at the cost of 32bit per node.

Conclusion

Persistent data structures preserve previous states after update operations, hence the name persistent. This property makes data structures effectively immutable and thus very well suited in concurrent environmens. The usage of a trie structure enables structural sharing, i.e. large parts of the data structure can be be safely shared between different versions. Performance is comparable to conventional mutable data structures where operations are in-place modifications. Update operations on immutable persistent data structures as described in this post have a worst-case time complexity of log32n, which is 2 for 1’000 and 7 for a 1’000’000’000 elements. This is so close to constant time that no difference in performance will be noticable in most applicatoins.

Other Resources

Vavr
Vavr is a functional library for Java. It provides immutable persistent collections and the necessary functions and control structures to operate on the values within the collections.

React.js Conf 2015 - Immutable Data and React.
Good talk by Lee Byron, the author of immutables.js. Lots of visual and code examples on how immutable persistent data structures work.

Michael J. Steindorfer, Efficient Immutable Collections
PhD thesis of Michael J. Steindorfer exploring immutable persistent data structures beyond HAMTs.

Scala immutable collections
Implementations of Scala’s immutable collections.

References